22. A Problem that Stumped Milton Friedman#

22.1. Overview#

This is the first of two lectures about a statistical decision problem that a US Navy Captain presented to Milton Friedman and W. Allen Wallis during World War II when they were analysts at the U.S. Government’s Statistical Research Group at Columbia University.

This problem led Abraham Wald [Wald, 1947] to formulate sequential analysis, an approach to statistical decision problems that is intimately related to dynamic programming.

In the spirit of this lecture, the present lecture and its sequel approach the problem from two distinct points of view.

In this lecture, we describe Wald’s formulation of the problem from the perspective of a statistician working within the Neyman-Pearson tradition of a frequentist statistician who thinks about testing hypotheses and consequently use laws of large numbers to investigate limiting properties of particular statistics under a given hypothesis, i.e., a vector of parameters that pins down a particular member of a manifold of statistical models that interest the statistician.

• From this lecture, please remember that a frequentist statistician routinely calculates functions of sequences of random variables, conditioning on a vector of parameters.

In this sequel we’ll discuss another formulation that adopts the perspective of a Bayesian statistician who views parameter vectors as vectors of random variables that are jointly distributed with observable variables that he is concerned about.

Because we are taking a frequentist perspective that is concerned about relative frequencies conditioned on alternative parameter values, i.e., alternative hypotheses, key ideas in this lecture

• Type I and type II statistical errors

  • a type I error occurs when you reject a null hypothesis that is true

  • a type II error occures when you accept a null hypothesis that is false

• Abraham Wald’s sequential probability ratio test

• The power of a frequentist statistical test

• The size of a frequentist statistical test

• The critical region of a statistical test

• A uniformly most powerful test

• The role of a Law of Large Numbers (LLN) in interpreting power and size of a frequentist statistical test

We’ll begin with some imports:

import numpy as np
import matplotlib.pyplot as plt
from numba import njit, prange
from numba.experimental import jitclass
from math import gamma
from scipy.integrate import quad
from scipy.stats import beta
from collections import namedtuple
import pandas as pd

This lecture uses ideas studied in this lecture and this lecture.

22.2. Source of the Problem#

On pages 137-139 of his 1998 book Two Lucky People with Rose Friedman [Friedman and Friedman, 1998], Milton Friedman described a problem presented to him and Allen Wallis during World War II, when they worked at the US Government’s Statistical Research Group at Columbia University.

Let’s listen to Milton Friedman tell us what happened

In order to understand the story, it is necessary to have an idea of a simple statistical problem, and of the standard procedure for dealing with it. The actual problem out of which sequential analysis grew will serve. The Navy has two alternative designs (say A and B) for a projectile. It wants to determine which is superior. To do so it undertakes a series of paired firings. On each round, it assigns the value 1 or 0 to A accordingly as its performance is superior or inferior to that of B and conversely 0 or 1 to B. The Navy asks the statistician how to conduct the test and how to analyze the results.

The standard statistical answer was to specify a number of firings (say 1,000) and a pair of percentages (e.g., 53% and 47%) and tell the client that if A receives a 1 in more than 53% of the firings, it can be regarded as superior; if it receives a 1 in fewer than 47%, B can be regarded as superior; if the percentage is between 47% and 53%, neither can be so regarded.

When Allen Wallis was discussing such a problem with (Navy) Captain Garret L. Schyler, the captain objected that such a test, to quote from Allen’s account, may prove wasteful. If a wise and seasoned ordnance officer like Schyler were on the premises, he would see after the first few thousand or even few hundred [rounds] that the experiment need not be completed either because the new method is obviously inferior or because it is obviously superior beyond what was hoped for $\dots$.

Friedman and Wallis worked on the problem but, after realizing that they were not able to solve it, they described the problem to Abraham Wald.

That started Wald on the path that led him to Sequential Analysis [Wald, 1947].

22.3. Neyman-Pearson Formulation#

It is useful to begin by describing the theory underlying the test that Navy Captain G. S. Schuyler had been told to use and that led him to approach Milton Friedman and Allan Wallis to convey his conjecture that superior practical procedures existed.

Evidently, the Navy had told Captain Schuyler to use what was then a state-of-the-art Neyman-Pearson hypothesis test.

We’ll rely on Abraham Wald’s [Wald, 1947] elegant summary of Neyman-Pearson theory.

Watch for these features of the setup:

• the assumption of a fixed sample size $n$

• the application of laws of large numbers, conditioned on alternative probability models, to interpret probabilities $\alpha$ and $\beta$ of the type I and type II errors defined in the Neyman-Pearson theory

In chapter 1 of Sequential Analysis [Wald, 1947] Abraham Wald summarizes the Neyman-Pearson approach to hypothesis testing.

Wald frames the problem as making a decision about a probability distribution that is partially known.

(You have to assume that something is already known in order to state a well-posed problem – usually, something means a lot)

By limiting what is unknown, Wald uses the following simple structure to illustrate the main ideas:

• A decision-maker wants to decide which of two distributions $f_0$, $f_1$ govern an IID random variable $z$.

• The null hypothesis $H_0$ is the statement that $f_0$ governs the data.

• The alternative hypothesis $H_1$ is the statement that $f_1$ governs the data.

• The problem is to devise and analyze a test of hypothesis $H_0$ against the alternative hypothesis $H_1$ on the basis of a sample of a fixed number $n$ independent observations $z_1,z_2,\dots ,z_n$ of the random variable $z$.

To quote Abraham Wald,

A test procedure leading to the acceptance or rejection of the [null] hypothesis in question is simply a rule specifying, for each possible sample of size $n$, whether the [null] hypothesis should be accepted or rejected on the basis of the sample. This may also be expressed as follows: A test procedure is simply a subdivision of the totality of all possible samples of size $n$ into two mutually exclusive parts, say part 1 and part 2, together with the application of the rule that the [null] hypothesis be accepted if the observed sample is contained in part 2. Part 1 is also called the critical region. Since part 2 is the totality of all samples of size $n$ which are not included in part 1, part 2 is uniquely determined by part 1. Thus, choosing a test procedure is equivalent to determining a critical region.

Let’s listen to Wald longer:

As a basis for choosing among critical regions the following considerations have been advanced by Neyman and Pearson: In accepting or rejecting $H_0$ we may commit errors of two kinds. We commit an error of the first kind if we reject $H_0$ when it is true; we commit an error of the second kind if we accept $H_0$ when $H_1$ is true. After a particular critical region $W$ has been chosen, the probability of committing an error of the first kind, as well as the probability of committing an error of the second kind is uniquely determined. The probability of committing an error of the first kind is equal to the probability, determined by the assumption that $H_0$ is true, that the observed sample will be included in the critical region $W$. The probability of committing an error of the second kind is equal to the probability, determined on the assumption that $H_1$ is true, that the probability will fall outside the critical region $W$. For any given critical region $W$ we shall denote the probability of an error of the first kind by $\alpha$ and the probability of an error of the second kind by $\beta$.

Let’s listen carefully to how Wald applies law of large numbers to interpret $\alpha$ and $\beta$:

The probabilities $\alpha$ and $\beta$ have the following important practical interpretation: Suppose that we draw a large number of samples of size $n$. Let $M$ be the number of such samples drawn. Suppose that for each of these $M$ samples we reject $H_0$ if the sample is included in $W$ and accept $H_0$ if the sample lies outside $W$. In this way we make $M$ statements of rejection or acceptance. Some of these statements will in general be wrong. If $H_0$ is true and if $M$ is large, the probability is nearly $1$ (i.e., it is practically certain) that the proportion of wrong statements (i.e., the number of wrong statements divided by $M$) will be approximately $\alpha$. If $H_1$ is true, the probability is nearly $1$ that the proportion of wrong statements will be approximately $\beta$. Thus, we can say that in the long run [ here Wald applies law of large numbers by driving $M\to \mathrm{\infty }$ (our comment, not Wald’s) ] the proportion of wrong statements will be $\alpha$ if $H_0$is true and $\beta$ if $H_1$ is true.

The quantity $\alpha$ is called the size of the critical region, and the quantity $1-\beta$ is called the power of the critical region.

Wald notes that

one critical region $W$ is more desirable than another if it has smaller values of $\alpha$ and $\beta$. Although either $\alpha$ or $\beta$ can be made arbitrarily small by a proper choice of the critical region $W$, it is possible to make both $\alpha$ and $\beta$ arbitrarily small for a fixed value of $n$, i.e., a fixed sample size.

Wald summarizes Neyman and Pearson’s setup as follows:

Neyman and Pearson show that a region consisting of all samples $(z_1,z_2,\dots ,z_n)$ which satisfy the inequality

$$\frac{f_1(z_1)\cdots f_1(z_n)}{f_0(z_1)\cdots f_0(z_n)}\ge k$$

is a most powerful critical region for testing the hypothesis $H_0$ against the alternative hypothesis $H_1$. The term $k$ on the right side is a constant chosen so that the region will have the required size $\alpha$.

Wald goes on to discuss Neyman and Pearson’s concept of uniformly most powerful test.

Here is how Wald introduces the notion of a sequential test

A rule is given for making one of the following three decisions at any stage of the experiment (at the m th trial for each integral value of m ): (1) to accept the hypothesis H , (2) to reject the hypothesis H , (3) to continue the experiment by making an additional observation. Thus, such a test procedure is carried out sequentially. On the basis of the first observation, one of the aforementioned decision is made. If the first or second decision is made, the process is terminated. If the third decision is made, a second trial is performed. Again, on the basis of the first two observations, one of the three decision is made. If the third decision is made, a third trial is performed, and so on. The process is continued until either the first or the second decisions is made. The number n of observations required by such a test procedure is a random variable, since the value of n depends on the outcome of the observations.

22.4. Wald’s Sequential Formulation#

In contradistinction to Neyman and Pearson’s formulation of the problem, in Wald’s formulation

• The sample size $n$ is not fixed but rather a random variable.

• Two parameters $A$ and $B$ that are related to but distinct from Neyman and Pearson’s $\alpha$ and $\beta$; $A$ and $B$ characterize cut-off rules that Wald uses to determine the random variable $n$ as a function of random outcomes.

Here is how Wald sets up the problem.

A decision-maker can observe a sequence of draws of a random variable $z$.

He (or she) wants to know which of two probability distributions $f_0$ or $f_1$ governs $z$.

To illustrate, let’s inspect some beta distributions.

The density of a Beta probability distribution with parameters $a$ and $b$ is

The next figure shows two beta distributions.

@njit
def p(x, a, b):
    r = gamma(a + b) / (gamma(a) * gamma(b))
    return r * x**(a-1) * (1 - x)**(b-1)

f0 = lambda x: p(x, 1, 1)
f1 = lambda x: p(x, 9, 9)
grid = np.linspace(0, 1, 50)

fig, ax = plt.subplots(figsize=(10, 8))

ax.set_title("Original Distributions")
ax.plot(grid, f0(grid), lw=2, label="$f_0$")
ax.plot(grid, f1(grid), lw=2, label="$f_1$")

ax.legend()
ax.set(xlabel="$z$ values", ylabel="probability of $z_k$")

plt.tight_layout()
plt.show()

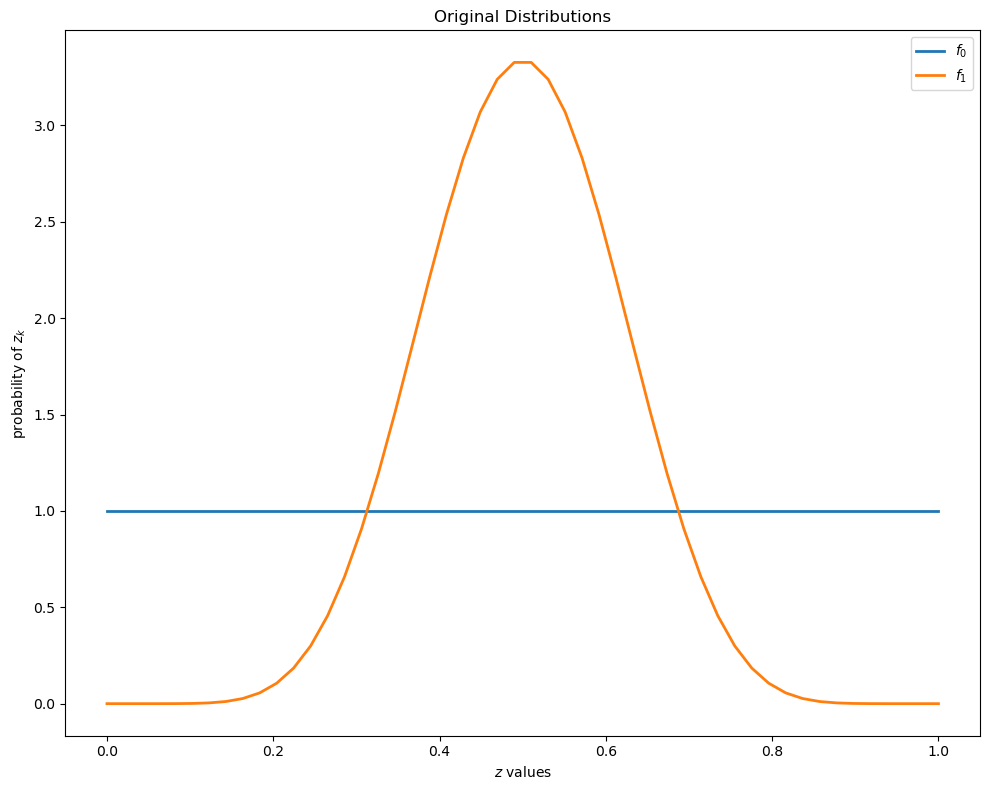
Conditional on knowing that successive observations are drawn from distribution $f_0$, the sequence of random variables is independently and identically distributed (IID).

Conditional on knowing that successive observations are drawn from distribution $f_1$, the sequence of random variables is also independently and identically distributed (IID).

But the observer does not know which of the two distributions generated the sequence.

For reasons explained in Exchangeability and Bayesian Updating, this means that the sequence is not IID.

The observer has something to learn, namely, whether the observations are drawn from $f_0$ or from $f_1$.

The decision maker wants to decide which of the two distributions is generating outcomes.

22.4.2. Choices#

After observing $z_k,z_{k-1},\dots ,z_0$, the decision-maker chooses among three distinct actions:

• He decides that $f=f_0$ and draws no more $z$’s

• He decides that $f=f_1$ and draws no more $z$’s

• He postpones deciding now and instead chooses to draw a $z_{k+1}$

Wald proceeds as follows.

He defines

• $p_{0m}=f_0(z_0)\cdots f_0(z_m)$

• $p_{1m}=f_1(z_0)\cdots f_1(z_m)$

• $L_m=\frac{p_{1m}}{p_{0m}}$

Here $\{L_m{\}}_{m=0}^{\mathrm{\infty }}$ is a likelihood ratio process.

One of Wald’s sequential decision rule is parameterized by two real numbers $B<A$.

For a given pair $A,B$ the decision rule is

$$\begin{array}{r}\begin{array}{c}\text{ accept }f=f_1\text{ if }{L}_m\ge A\\ \text{ accept }f=f_0\text{ if }{L}_m\le B\\ \text{ draw another }z\text{ if }B<L_m<A\end{array}\end{array}$$

The following figure illustrates aspects of Wald’s procedure.

22.5. Links Between $A,B$ and $\alpha ,\beta$#

In chapter 3 of Sequential Analysis [Wald, 1947] Wald establishes the inequalities

His analysis of these inequalities leads Wald to recommend the following approximations as rules for setting $A$ and $B$ that come close to attaining a decision maker’s target values for probabilities $\alpha$ of a type I and $\beta$ of a type II error:

For small values of $\alpha$ and $\beta$, Wald shows that approximation (22.1) provides a good way to set $A$ and $B$.

In particular, Wald constructs a mathematical argument that leads him to conclude that the use of approximation (22.1) rather than the true functions $A(\alpha ,\beta ),B(\alpha ,\beta )$ for setting $A$ and $B$

$\dots$ cannot result in any appreciable increase in the value of either $\alpha$ or $\beta$. In other words, for all practical purposes the test corresponding to $A=a(\alpha ,\beta ),B=b(\alpha ,\beta )$ provides as least the same protection against wrong decisions as the test corresponding to $A=A(\alpha ,\beta )$ and $B=b(\alpha ,\beta )$.

Thus, the only disadvantage that may arise from using $a(\alpha ,\beta ),b(\alpha ,\beta )$ instead of $A(\alpha ,\beta ),B(\alpha ,\beta )$, respectively, is that it may result in an appreciable increase in the number of observations required by the test.

22.6. Simulations#

In this section, we experiment with different distributions $f_0$ and $f_1$ to examine how Wald’s test performs under various conditions.

The goal of these simulations is to understand trade-offs between decision speed and accuracy associated with Wald’s sequential probability ratio test.

Specifically, we will watch how:

• The decision thresholds $A$ and $B$ (or equivalently the target error rates $\alpha$ and $\beta$) affect the average stopping time

• The discrepancy between distributions $f_0$ and $f_1$ affects average stopping times

We will focus on the case where $f_0$ and $f_1$ are beta distributions since it is easy to control the overlapping regions of the two densities by adjusting their shape parameters.

First, we define a namedtuple to store all the parameters we need for our simulation studies.

SPRTParams = namedtuple('SPRTParams', 
                ['α', 'β',  # Target type I and type II errors
                'a0', 'b0', # Shape parameters for f_0
                'a1', 'b1', # Shape parameters for f_1
                'N',        # Number of simulations
                'seed'])

Now we can run the simulation following Wald’s recommendation.

We use the log-likelihood ratio and compare it to the logarithms of the thresholds $\log (A)$ and $\log (B)$.

Below is the algorithm for the simulation.

1. Compute thresholds $A=\frac{1-\beta }{\alpha }$, $B=\frac{\beta }{1-\alpha }$ and work with $\log A$, $\log B$.

2. Given true distribution (either $f_0$ or $f_1$):

   • Initialize log-likelihood ratio $\log L_0=0$

   • Repeat:

     • Draw observation $z$ from the true distribution

     • Update: $\log L_{n+1}\leftarrow \log L_n+(\log f_1(z)-\log f_0(z))$

     • If $\log L_{n+1}\ge \log A$: stop, reject $H_0$

     • If $\log L_{n+1}\le \log B$: stop, accept $H_0$

3. Repeat step 2 for $N$ replications with $N/2$ replications for each distribution, compute the empirical type I error $\hat{\alpha }$ and type II error $\hat{\beta }$ with

@njit
def sprt_single_run(a0, b0, a1, b1, logA, logB, true_f0, seed):
    """Run a single SPRT until a decision is reached."""
    log_L = 0.0
    n = 0
    
    # Set seed for this run
    np.random.seed(seed)
    
    while True:
        # Draw a random variable from the appropriate distribution
        if true_f0:
            z = np.random.beta(a0, b0)
        else:
            z = np.random.beta(a1, b1)
        
        n += 1
        
        # Update the log-likelihood ratio
        log_f1_z = np.log(p(z, a1, b1))
        log_f0_z = np.log(p(z, a0, b0))
        log_L += log_f1_z - log_f0_z
        
        # Check stopping conditions
        if log_L >= logA:
            return n, False  # Reject H0
        elif log_L <= logB:
            return n, True   # Accept H0

@njit(parallel=True)
def run_sprt_simulation(a0, b0, a1, b1, alpha, βs, N, seed):
    """SPRT simulation described by the algorithm."""
    
    # Calculate thresholds
    A = (1 - βs) / alpha
    B = βs / (1 - alpha)
    logA = np.log(A)
    logB = np.log(B)
    
    # Pre-allocate arrays
    stopping_times = np.zeros(N, dtype=np.int64)

    # Store decision and ground truth as boolean arrays
    decisions_h0 = np.zeros(N, dtype=np.bool_)
    truth_h0 = np.zeros(N, dtype=np.bool_)
    
    # Run simulations in parallel
    for i in prange(N):
        true_f0 = (i % 2 == 0)
        truth_h0[i] = true_f0
        
        n, accept_f0 = sprt_single_run(
                            a0, b0, a1, b1, 
                            logA, logB, 
                            true_f0, seed + i)

        stopping_times[i] = n
        decisions_h0[i] = accept_f0
    
    return stopping_times, decisions_h0, truth_h0

def run_sprt(params):
    """Run SPRT simulations with given parameters."""
    
    stopping_times, decisions_h0, truth_h0 = run_sprt_simulation(
        params.a0, params.b0, params.a1, params.b1, 
        params.α, params.β, params.N, params.seed
    )
    
    # Calculate error rates
    truth_h0_bool = truth_h0.astype(bool)
    decisions_h0_bool = decisions_h0.astype(bool)

    # For type I error: P(reject H0 | H0 is true)
    type_I = np.sum(truth_h0_bool 
                    & ~decisions_h0_bool) / np.sum(truth_h0_bool)
    
    # For type II error: P(accept H0 | H0 is false)  
    type_II = np.sum(~truth_h0_bool 
                    & decisions_h0_bool) / np.sum(~truth_h0_bool)
    
    # Create scipy distributions for compatibility
    f0 = beta(params.a0, params.b0)
    f1 = beta(params.a1, params.b1)
    
    return {
        'stopping_times': stopping_times,
        'decisions_h0': decisions_h0_bool,
        'truth_h0': truth_h0_bool,
        'type_I': type_I,
        'type_II': type_II,
        'f0': f0,
        'f1': f1
    }
    
# Run simulation
params = SPRTParams(α=0.05, β=0.10, a0=2, b0=5, a1=5, b1=2, N=20000, seed=1)
results = run_sprt(params)

print(f"Average stopping time: {results['stopping_times'].mean():.2f}")
print(f"Empirical type I  error: {results['type_I']:.3f}   (target = {params.α})")
print(f"Empirical type II error: {results['type_II']:.3f}   (target = {params.β})")

Average stopping time: 1.59
Empirical type I  error: 0.012   (target = 0.05)
Empirical type II error: 0.022   (target = 0.1)

As anticipated in the passage above in which Wald discussed the quality of $a(\alpha ,\beta ),b(\alpha ,\beta )$ given in approximation (22.1), we find that the algorithm “overshoots” the error rates by giving us a lower type I and type II error rates than the target values.

The following code constructs a graph that lets us visualize two distributions and the distribution of times to reach a decision.

fig, axes = plt.subplots(1, 2, figsize=(14, 5))

z_grid = np.linspace(0, 1, 200)
axes[0].plot(z_grid, results['f0'].pdf(z_grid), 'b-', 
             lw=2, label=f'$f_0 = \\text{{Beta}}({params.a0},{params.b0})$')
axes[0].plot(z_grid, results['f1'].pdf(z_grid), 'r-', 
             lw=2, label=f'$f_1 = \\text{{Beta}}({params.a1},{params.b1})$')
axes[0].fill_between(z_grid, 0, 
                     np.minimum(results['f0'].pdf(z_grid), 
                                results['f1'].pdf(z_grid)), 
                     alpha=0.3, color='purple', label='overlap region')
axes[0].set_xlabel('z')
axes[0].set_ylabel('density')
axes[0].legend()

axes[1].hist(results['stopping_times'], 
             bins=np.arange(1, results['stopping_times'].max() + 1.5) - 0.5,
            color="steelblue", alpha=0.8, edgecolor="black")
axes[1].set_title("distribution of stopping times $n$")
axes[1].set_xlabel("$n$")
axes[1].set_ylabel("frequency")

plt.show()

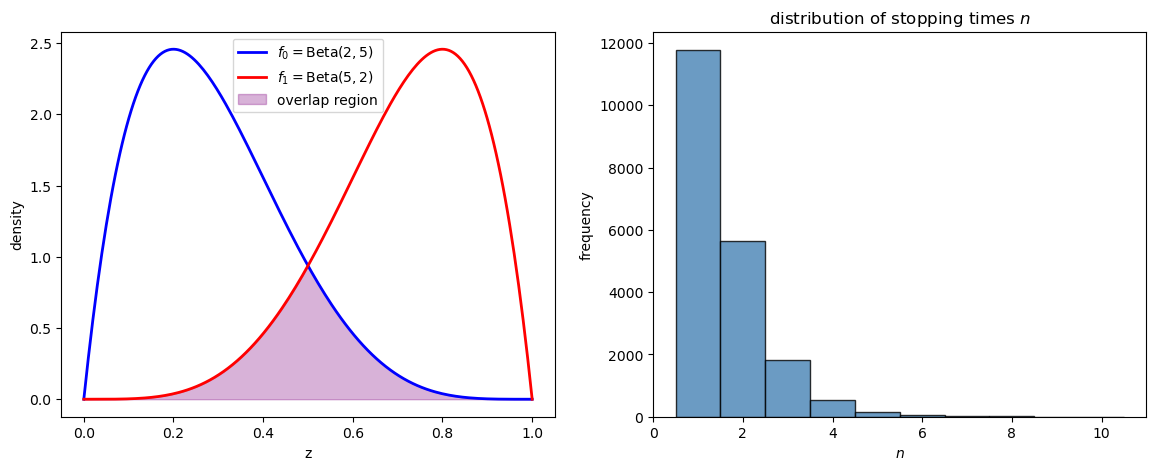
In this simple case, the stopping time stays below 10.

We can also examine a $2\times 2$ “confusion matrix” whose diagonal elements show the number of times when Wald’s rule results in correct acceptance and rejection of the null hypothesis.

# Accept H0 when H0 is true (correct)
f0_correct = np.sum(results['truth_h0'] & results['decisions_h0'])

# Reject H0 when H0 is true (incorrect)
f0_incorrect = np.sum(results['truth_h0'] & (~results['decisions_h0']))

# Reject H0 when H1 is true (correct)
f1_correct = np.sum((~results['truth_h0']) & (~results['decisions_h0']))

# Accept H0 when H1 is true (incorrect)
f1_incorrect = np.sum((~results['truth_h0']) & results['decisions_h0'])

# First row is when f0 is the true distribution
# Second row is when f1 is true
confusion_data = np.array([[f0_correct, f0_incorrect],
                          [f1_incorrect, f1_correct]])

row_totals = confusion_data.sum(axis=1, keepdims=True)

print("Confusion Matrix:")
print(confusion_data)

fig, ax = plt.subplots()
ax.imshow(confusion_data, cmap='Blues', aspect='equal')
ax.set_xticks([0, 1])
ax.set_xticklabels(['accept $H_0$', 'reject $H_0$'])
ax.set_yticks([0, 1])
ax.set_yticklabels(['true $f_0$', 'true $f_1$'])

for i in range(2):
    for j in range(2):
        percent = confusion_data[i, j] / row_totals[i, 0] if row_totals[i, 0] > 0 else 0
        color = 'white' if confusion_data[i, j] > confusion_data.max() * 0.5 else 'black'
        ax.text(j, i, f'{confusion_data[i, j]}\n({percent:.1%})',
                      ha="center", va="center", 
                      color=color, fontweight='bold')
plt.tight_layout()
plt.show()

Confusion Matrix:
[[9879  121]
 [ 225 9775]]

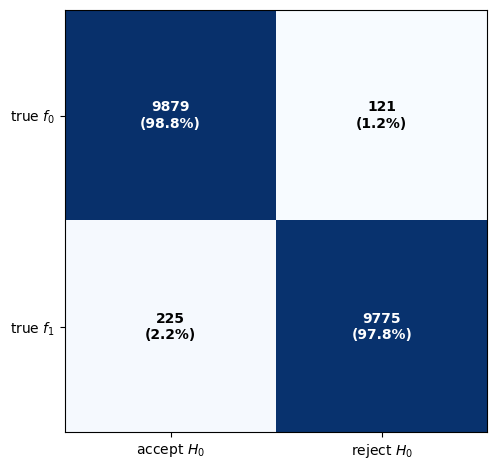
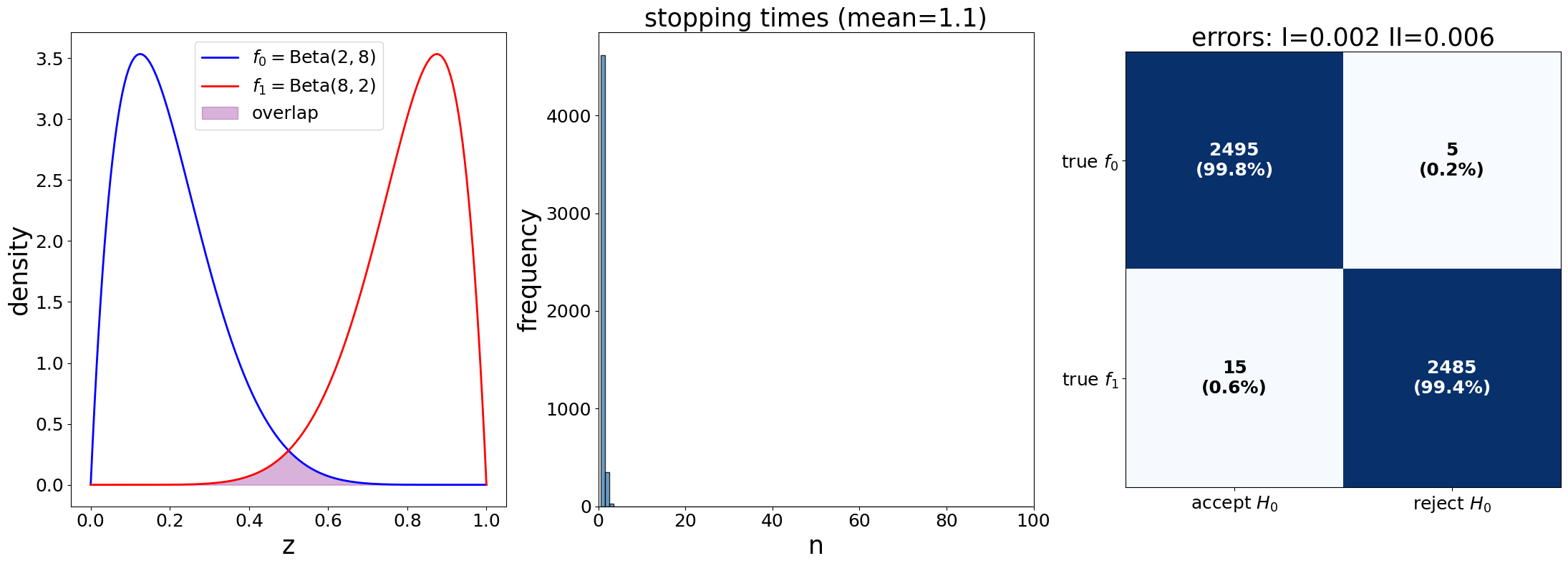
Next we use our code to study three different $f_0,f_1$ pairs having different discrepancies between distributions.

We plot the same three graphs we used above for each pair of distributions

params_1 = SPRTParams(α=0.05, β=0.10, a0=2, b0=8, a1=8, b1=2, N=5000, seed=42)
results_1 = run_sprt(params_1)

params_2 = SPRTParams(α=0.05, β=0.10, a0=4, b0=5, a1=5, b1=4, N=5000, seed=42)
results_2 = run_sprt(params_2)

params_3 = SPRTParams(α=0.05, β=0.10, a0=0.5, b0=0.4, a1=0.4, 
                      b1=0.5, N=5000, seed=42)
results_3 = run_sprt(params_3)

def plot_sprt_results(results, params, title=""):
    """Plot SPRT simulation results."""
    fig, axes = plt.subplots(1, 3, figsize=(22, 8))
    
    # Distribution plots
    z_grid = np.linspace(0, 1, 200)
    axes[0].plot(z_grid, results['f0'].pdf(z_grid), 'b-', lw=2, 
                     label=f'$f_0 = \\text{{Beta}}({params.a0},{params.b0})$')
    axes[0].plot(z_grid, results['f1'].pdf(z_grid), 'r-', lw=2, 
                     label=f'$f_1 = \\text{{Beta}}({params.a1},{params.b1})$')
    axes[0].fill_between(z_grid, 0, 
                np.minimum(results['f0'].pdf(z_grid), results['f1'].pdf(z_grid)), 
                alpha=0.3, color='purple', label='overlap')
    if title:
        axes[0].set_title(title, fontsize=25)
    axes[0].set_xlabel('z', fontsize=25)
    axes[0].set_ylabel('density', fontsize=25)
    axes[0].legend(fontsize=18)
    axes[0].tick_params(axis='both', which='major', labelsize=18)
    
    # Stopping times
    max_n = max(results['stopping_times'].max(), 101)
    bins = np.arange(1, min(max_n, 101)) - 0.5
    axes[1].hist(results['stopping_times'], bins=bins, 
                     color="steelblue", alpha=0.8, edgecolor="black")
    axes[1].set_title(f'stopping times (mean={results["stopping_times"].mean():.1f})', 
                    fontsize=25)
    axes[1].set_xlabel('n', fontsize=25)
    axes[1].set_ylabel('frequency', fontsize=25)
    axes[1].set_xlim(0, 100)
    axes[1].tick_params(axis='both', which='major', labelsize=18)
    
    # Confusion matrix
    f0_correct = np.sum(results['truth_h0'] & results['decisions_h0'])
    f0_incorrect = np.sum(results['truth_h0'] & (~results['decisions_h0']))
    f1_correct = np.sum((~results['truth_h0']) & (~results['decisions_h0']))
    f1_incorrect = np.sum((~results['truth_h0']) & results['decisions_h0'])
    
    confusion_data = np.array([[f0_correct, f0_incorrect], 
                              [f1_incorrect, f1_correct]])
    row_totals = confusion_data.sum(axis=1, keepdims=True)
    
    im = axes[2].imshow(confusion_data, cmap='Blues', aspect='equal')
    axes[2].set_title(f'errors: I={results["type_I"]:.3f} '+ 
                      f'II={results["type_II"]:.3f}', fontsize=25)
    axes[2].set_xticks([0, 1])
    axes[2].set_xticklabels(['accept $H_0$', 'reject $H_0$'], fontsize=22)
    axes[2].set_yticks([0, 1])
    axes[2].set_yticklabels(['true $f_0$', 'true $f_1$'], fontsize=22)
    axes[2].tick_params(axis='both', which='major', labelsize=18)

    
    for i in range(2):
        for j in range(2):
            percent = confusion_data[i, j] / row_totals[i, 0] if row_totals[i, 0] > 0 else 0
            color = 'white' if confusion_data[i, j] > confusion_data.max() * 0.5 else 'black'
            axes[2].text(j, i, f'{confusion_data[i, j]}\n({percent:.1%})',
                             ha="center", va="center", 
                             color=color, fontweight='bold', 
                             fontsize=18)

    plt.tight_layout()
    plt.show()

plot_sprt_results(results_1, params_1)

plot_sprt_results(results_2, params_2)

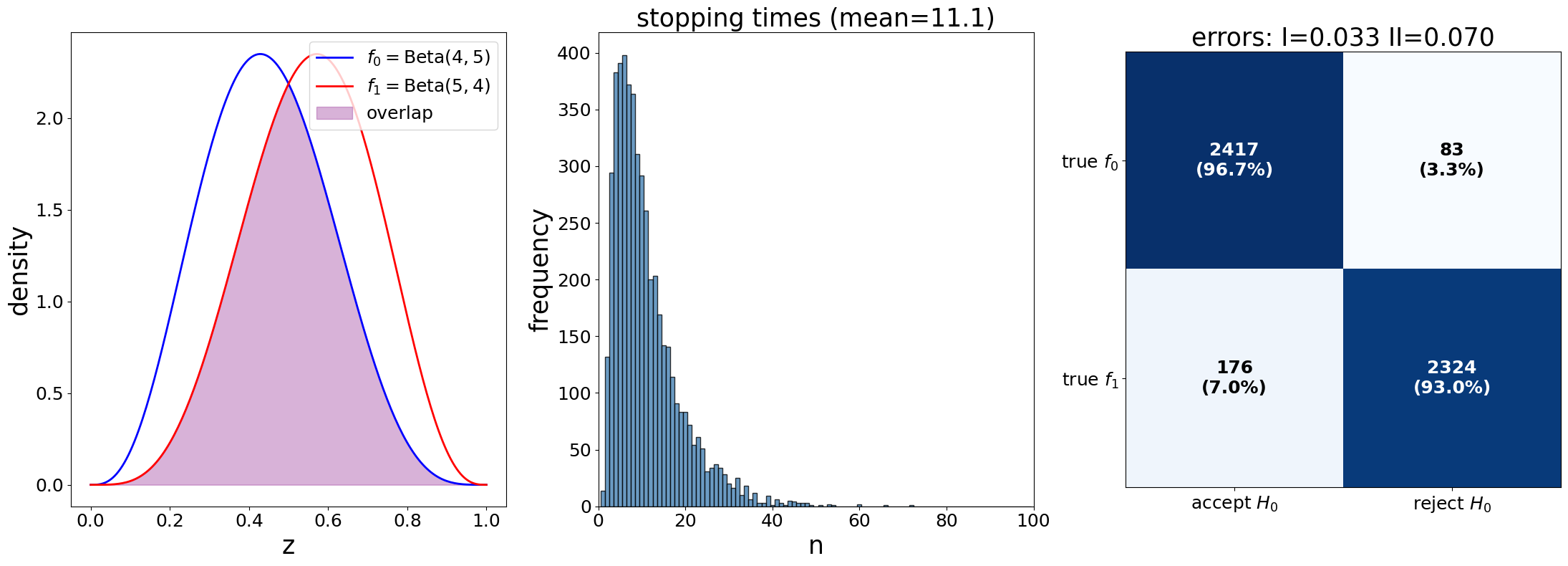
plot_sprt_results(results_3, params_3)

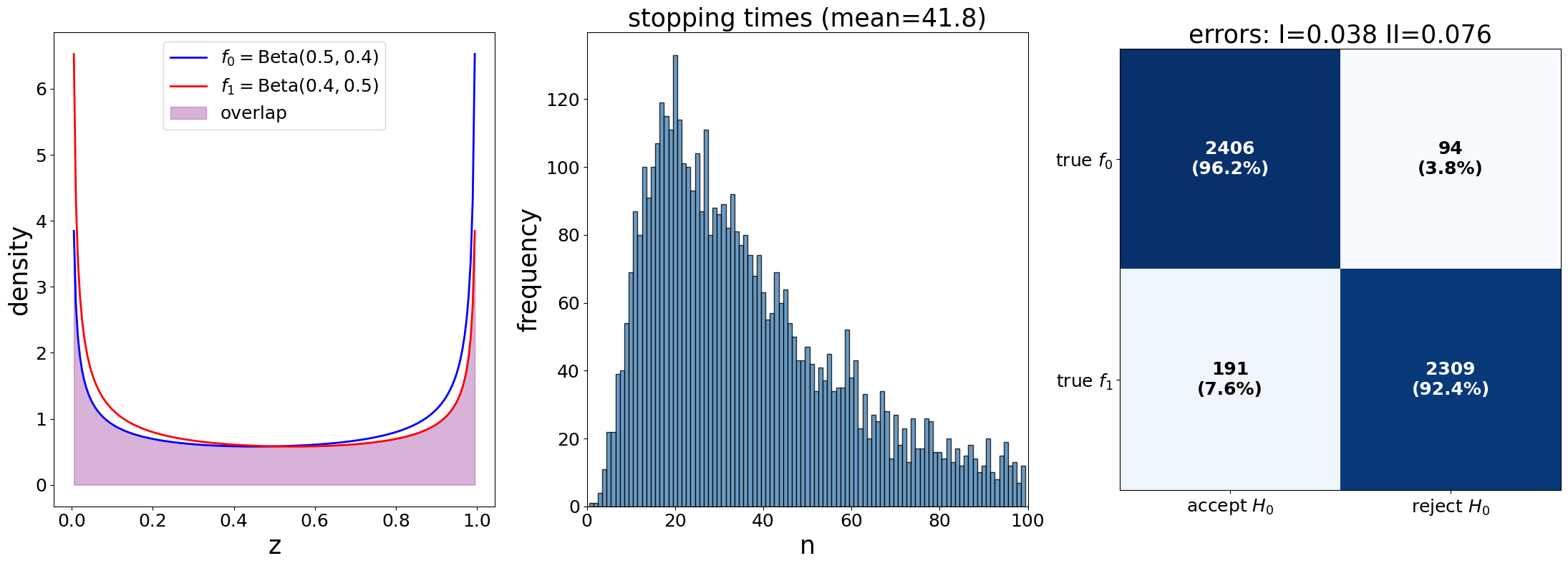
We can see a clear pattern in the stopping times and how close “separated” the two distributions are.

We can link this to the discussion of Kullback–Leibler divergence in this lecture.

Intuitively, KL divergence is large when the distribution from one distribution to another is large.

When two distributions are “far apart”, it should not take long to decide which one is generating the data.

When two distributions are “close” to each other, it takes longer to decide which one is generating the data.

However, KL divergence is not symmetric, meaning that the divergence from one distribution to another is not necessarily the same as the reverse.

To measure the discrepancy between two distributions, we use a metric called Jensen-Shannon distance and plot it against the average stopping times.

def kl_div(h, f):
    """KL divergence"""
    integrand = lambda w: f(w) * np.log(f(w) / h(w))
    val, _ = quad(integrand, 0, 1)
    return val

def js_dist(a0, b0, a1, b1):
    """Jensen–Shannon distance"""
    f0 = lambda w: p(w, a0, b0)
    f1 = lambda w: p(w, a1, b1)

    # Mixture
    m = lambda w: 0.5*(f0(w) + f1(w))
    return np.sqrt(0.5*kl_div(m, f0) + 0.5*kl_div(m, f1))
    
def generate_β_pairs(N=100, T=10.0, d_min=0.5, d_max=9.5):
    ds = np.linspace(d_min, d_max, N)
    a0 = (T - ds) / 2
    b0 = (T + ds) / 2
    return list(zip(a0, b0, b0, a0))

param_comb = generate_β_pairs()

# Run simulations for each parameter combination
js_dists = []
mean_stopping_times = []
param_list = []

for a0, b0, a1, b1 in param_comb:
    # Compute KL divergence
    js_div = js_dist(a1, b1, a0, b0)
    
    # Run SPRT simulation with a fixed set of parameters d d
    params = SPRTParams(α=0.05, β=0.10, a0=a0, b0=b0, 
                        a1=a1, b1=b1, N=5000, seed=42)
    results = run_sprt(params)
    
    js_dists.append(js_div)
    mean_stopping_times.append(results['stopping_times'].mean())
    param_list.append((a0, b0, a1, b1))

# Create the plot
fig, ax = plt.subplots(figsize=(6, 6))

scatter = ax.scatter(js_dists, mean_stopping_times, 
                    s=80, alpha=0.7, c=range(len(js_dists)),
                    linewidth=0.5)

ax.set_xlabel('Jensen–Shannon distance', fontsize=14)
ax.set_ylabel('mean stopping time', fontsize=14)

plt.tight_layout()
plt.show()

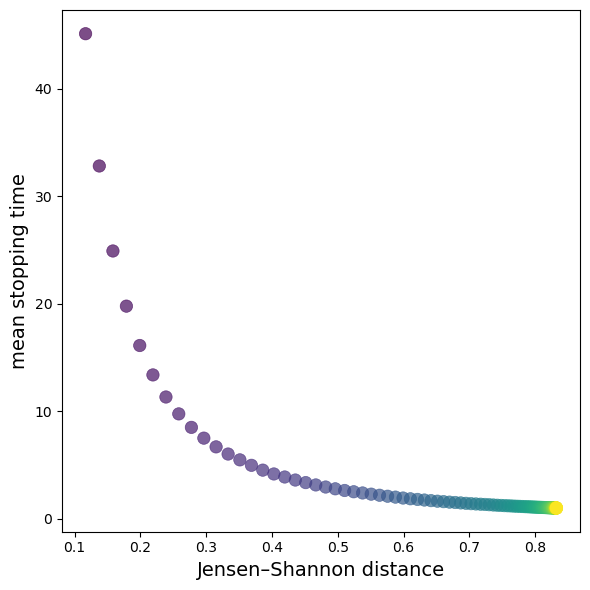
The plot demonstrates a clear negative correlation between relative entropy and mean stopping time.

As the KL divergence increases (distributions become more separated), the mean stopping time decreases exponentially.

Below are sampled examples from the experiments we have above

selected_indices = [0, 
                    len(param_comb)//6, 
                    len(param_comb)//3, 
                    len(param_comb)//2, 
                    2*len(param_comb)//3, 
                    -1]

fig, axes = plt.subplots(2, 3, figsize=(15, 8))

for i, idx in enumerate(selected_indices):
    row = i // 3
    col = i % 3
    
    a0, b0, a1, b1 = param_list[idx]
    js_dist = js_dists[idx]
    mean_time = mean_stopping_times[idx]
    
    # Plot the distributions
    z_grid = np.linspace(0, 1, 200)
    f0_dist = beta(a0, b0)
    f1_dist = beta(a1, b1)
    
    axes[row, col].plot(z_grid, f0_dist.pdf(z_grid), 'b-', 
                        lw=2, label='$f_0$')
    axes[row, col].plot(z_grid, f1_dist.pdf(z_grid), 'r-', 
                        lw=2, label='$f_1$')
    axes[row, col].fill_between(z_grid, 0, 
                        np.minimum(f0_dist.pdf(z_grid), 
                        f1_dist.pdf(z_grid)), 
                        alpha=0.3, color='purple')
    
    axes[row, col].set_title(f'JS dist: {js_dist:.3f}'
                +f'\nMean time: {mean_time:.1f}', fontsize=12)
    axes[row, col].set_xlabel('z', fontsize=10)
    if i == 0:
        axes[row, col].set_ylabel('density', fontsize=10)
        axes[row, col].legend(fontsize=10)


plt.tight_layout()
plt.show()

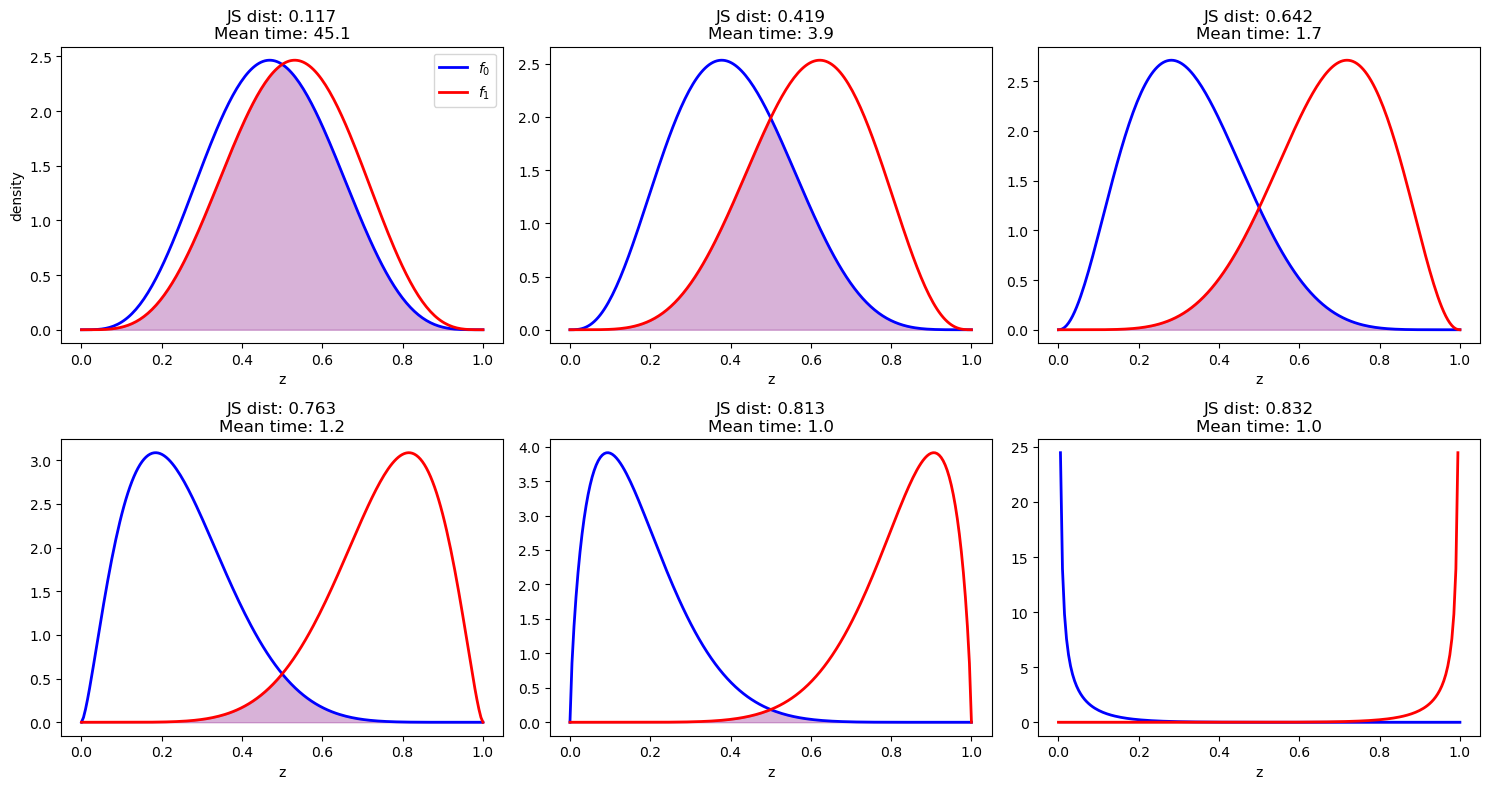
Again, we find that the stopping time is shorter when the distributions are more separated measured by Jensen-Shannon distance.

Let’s visualize individual likelihood ratio processes to see how they evolve toward the decision boundaries.

def plot_likelihood_paths(params, n_highlight=10, n_background=200):
    """Plot likelihood ratio paths"""
    
    A = (1 - params.β) / params.α
    B = params.β / (1 - params.α)
    logA, logB = np.log(A), np.log(B)
    
    f0 = beta(params.a0, params.b0)
    f1 = beta(params.a1, params.b1)
    
    fig, axes = plt.subplots(1, 2, figsize=(14, 7))
    
    # Generate and plot paths for each distribution
    for dist_idx, (true_f0, ax, title) in enumerate([
        (True, axes[0], 'true distribution: $f_0$'),
        (False, axes[1], 'true distribution: $f_1$')
    ]):
        rng = np.random.default_rng(seed=42 + dist_idx)
        paths_data = []
        
        for path in range(n_background + n_highlight):
            log_L_path = [0.0]  # Start at 0
            log_L = 0.0
            n = 0
            
            while True:
                z = f0.rvs(random_state=rng) if true_f0 else f1.rvs(random_state=rng)
                n += 1
                log_L += np.log(f1.pdf(z)) - np.log(f0.pdf(z))
                log_L_path.append(log_L)
                
                # Check stopping conditions
                if log_L >= logA or log_L <= logB:
                    # True = reject H0, False = accept H0
                    decision = log_L >= logA
                    break
            
            paths_data.append((log_L_path, n, decision))
        
        for i, (path, n, decision) in enumerate(paths_data[:n_background]):
            color = 'C1' if decision else 'C0'
            ax.plot(range(len(path)), path, 
                    color=color, alpha=0.2, linewidth=0.5)
        
        for i, (path, n, decision) in enumerate(paths_data[n_background:]):
            # Color code by decision
            color = 'C1' if decision else 'C0'
            ax.plot(range(len(path)), path, color=color, 
                    alpha=0.8, linewidth=1.5,
                    label='reject $H_0$' if decision and i == 0 else (
                    'accept $H_0$' if not decision and i == 0 else ''))
        
        ax.axhline(y=logA, color='C1', linestyle='--', linewidth=2, 
                  label=f'$\\log A = {logA:.2f}$')
        ax.axhline(y=logB, color='C0', linestyle='--', linewidth=2, 
                  label=f'$\\log B = {logB:.2f}$')
        ax.axhline(y=0, color='black', linestyle='-', 
                  alpha=0.5, linewidth=1)
        
        ax.set_xlabel(r'$n$')
        ax.set_ylabel(r'$log(L_n)$')
        ax.set_title(title, fontsize=20)
        ax.legend(fontsize=18, loc='center right')
        
        y_margin = max(abs(logA), abs(logB)) * 0.2
        ax.set_ylim(logB - y_margin, logA + y_margin)
    
    plt.tight_layout()
    plt.show()

plot_likelihood_paths(params_3, n_highlight=10, n_background=100)

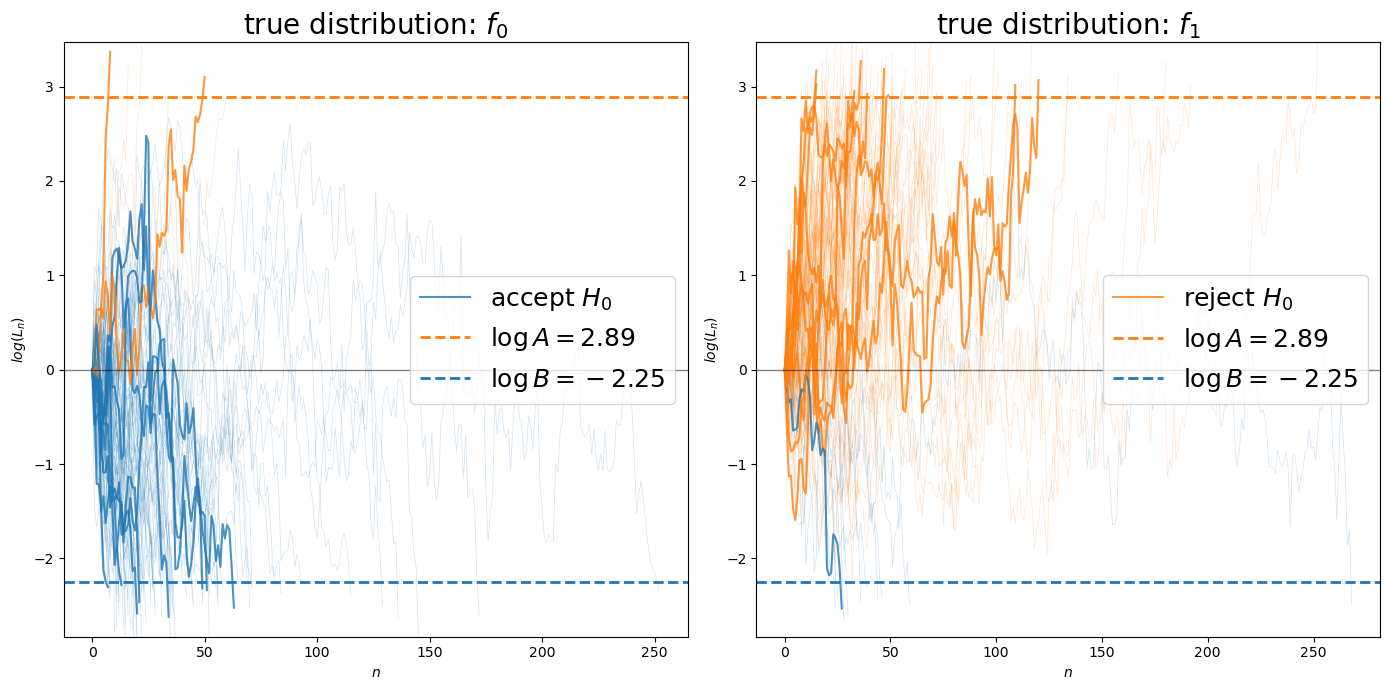
Next, let’s adjust the decision thresholds $A$ and $B$ and examine how the mean stopping time and the type I and type II error rates change.

In the code below, we break Wald’s rule by adjusting the thresholds $A$ and $B$ using factors $A_f$ and $B_f$.

@njit(parallel=True)  
def run_adjusted_thresholds(a0, b0, a1, b1, alpha, βs, N, seed, A_f, B_f):
    """SPRT simulation with adjusted thresholds."""
    
    # Calculate original thresholds  
    A_original = (1 - βs) / alpha
    B_original = βs / (1 - alpha)
    
    # Apply adjustment factors
    A_adj = A_original * A_f
    B_adj = B_original * B_f
    logA = np.log(A_adj)
    logB = np.log(B_adj)
    
    # Pre-allocate arrays
    stopping_times = np.zeros(N, dtype=np.int64)
    decisions_h0 = np.zeros(N, dtype=np.bool_)
    truth_h0 = np.zeros(N, dtype=np.bool_)
    
    # Run simulations in parallel
    for i in prange(N):
        true_f0 = (i % 2 == 0)
        truth_h0[i] = true_f0
        
        n, accept_f0 = sprt_single_run(a0, b0, a1, b1, 
                        logA, logB, true_f0, seed + i)
        stopping_times[i] = n
        decisions_h0[i] = accept_f0
    
    return stopping_times, decisions_h0, truth_h0, A_adj, B_adj

def run_adjusted(params, A_f=1.0, B_f=1.0):
    """Wrapper to run SPRT with adjusted A and B thresholds."""
    
    stopping_times, decisions_h0, truth_h0, A_adj, B_adj = run_adjusted_thresholds(
        params.a0, params.b0, params.a1, params.b1, 
        params.α, params.β, params.N, params.seed, A_f, B_f
    )
    truth_h0_bool = truth_h0.astype(bool)
    decisions_h0_bool = decisions_h0.astype(bool)
    
    # Calculate error rates
    type_I = np.sum(truth_h0_bool 
                    & ~decisions_h0_bool) / np.sum(truth_h0_bool)
    type_II = np.sum(~truth_h0_bool 
                    & decisions_h0_bool) / np.sum(~truth_h0_bool)
    
    return {
        'stopping_times': stopping_times,
        'type_I': type_I,
        'type_II': type_II,
        'A_used': A_adj,
        'B_used': B_adj
    }

adjustments = [
    (5.0, 0.5), 
    (1.0, 1.0),    
    (0.3, 3.0),    
    (0.2, 5.0),    
    (0.15, 7.0),   
]

results_table = []
for A_f, B_f in adjustments:
    result = run_adjusted(params_2, A_f, B_f)
    results_table.append([
        A_f, B_f, 
        f"{result['stopping_times'].mean():.1f}",
        f"{result['type_I']:.3f}",
        f"{result['type_II']:.3f}"
    ])

df = pd.DataFrame(results_table, 
                 columns=["A_f", "B_f", "mean stop time", 
                          "Type I error", "Type II error"])
df = df.set_index(["A_f", "B_f"])
df

Let’s pause and think about the table more carefully by referring back to (22.1).

Recall that $A=\frac{1-\beta }{\alpha }$ and $B=\frac{\beta }{1-\alpha }$.

When we multiply $A$ by a factor less than 1 (making $A$ smaller), we are effectively making it easier to reject the null hypothesis $H_0$.

This increases the probability of Type I errors.

When we multiply $B$ by a factor greater than 1 (making $B$ larger), we are making it easier to accept the null hypothesis $H_0$.

This increases the probability of Type II errors.

The table confirms this intuition: as $A$ decreases and $B$ increases from their optimal Wald values, both Type I and Type II error rates increase, while the mean stopping time decreases.

22.7. Related Lectures#

We’ll dig deeper into some of the ideas used here in the following earlier and later lectures:

• this sequel reformulates the problem from the perspective of a Bayesian statistician who views parameters as vectors of random variables that are jointly distributed with the observable that he is concerned about.

• this lecture discusses the key concept of exchangeability that underlies statistical learning

• this lecture describes likelihood ratio processes and their role in frequentist and Bayesian statistical theories

• this lecture discusses the role of likelihood ratio processes in Bayesian learning

• this lecture takes up the subject of this lecture and studies whether the Captain’s hunch that the (frequentist) decision rule that the Navy had ordered him to use can be expected to be better or worse than our sequential decision rule